头头
在现代密码学中我们经常接触到三个东西：摘要算法，非对称加密算法与对称加密算法。
摘要算法通过单向陷门函数将任意长度映射到固定长度，这个过程是不可逆的，再加上它的抗碰撞性让它成为标识数据的好方法，这方面如果用的算法是老古董就可能受碰撞和长度扩展攻击的影响。
对称加密算法使用的加解密钥相同，可再分为流密码与分组密码，流密码将它的密钥作为随机数种子通过伪随机生成函数源源不断地生成随机数，明文与之异或就得到了密文，由于异或运算的特性密文与之异或也就恢复了明文，因此它的加解密算法是一样的，而且它针对的任意长度的数据。分组密码的密钥和加密长度是固定的，它会对加密密钥进行一些变换，再与明文进行运算，该过程可能进行多次因此加解密算法不一定相同，由于它只能加密固定长度的数据，而一般要加密的数据长度都不满足要求，此时就需要把数据分组，若分组后最后一组的长度不满足要求又需要对其填充，前者就是分组密码的工作模式。是否需要填充也和工作模式相关，如OFB模式就可以将过程转换为类似流密码的方式，而XTS使用密文窃取也不需要填充，另外即使长度刚好符合也可能需要填充，如PKCS7此时就需要再填充一个完整的分组，之前提到若PKCS7与CBC模式组合时，就有可能出现PaddingOracle漏洞，即若服务端会返回解密状态则可以通过推测加密任何数据。
非对称加密算法加解密不再使用相同的密钥，而且它的结构和对称密码有很大的不同，对称密码更像是逻辑位运算而非对称是数学运算，它利用的全是数学上的难题，就是(给一个限制)后只有正向计算的算法，而还没有逆向计算的算法(大整数分解，椭圆曲线离散对数，格最短向量等)，先随机生成符合要求的私钥，私钥到公钥的生成过程是正向的有算法因此很容易，而反过来就没有算法可恢复，通过公开公钥就可实现加密与签名功能，由于这种加密也是在有限的范围上完成的因此单次运算的数字大小有限制，为此也需要对其分组填充，RSA就有PKCS1 V1.5与PKCS OAEP。
PKCS1-V1.5
它是针对RSA的公钥密码标准，定义了公私钥的数学属性，操作原语，操作方案等，当前最新版是RFC8017。我们在实际使用RSA时其实是使用这里面规定的操作方案，这里主要关注的是它的加解密部分，由于输入数据长度mLen不能大于模数n会导致解密出错，输入数据太小时会导致幂运算结果小于模数从而退化成非模幂运算(这种运算的逆运算是易解的)，因此它规定了一次加密的数据长度不能大于k-11，这里的k代表模数n的长度，之后对明文M做如下填充：
EM = 0x00 || 0x02 || PS || 0x00 || M
这里的EM是最终要被加密的明文，PS是随机生成的不小于8字节的内容不含0x00的数据，更准确的说PS的长度应该为k - mLen - 3，解密时，求出EM后，需要先判断数据的开头是否是0x00 0x02这表示是公钥加密，之后会读取余下数据，直到读到0x00表示PS结束，此时会判断PS的长度是否大于7，若小于等于7表示这个数据不符合规范，即解密出错，若正确余下的就是明文M。
误用
密码学中最常见的问题就是误用，如下两篇文章描述了关于PKCS V1.5误用的一些例子：
- Google CTF 2017 Crypto 201 RSA CTF Challenge
- What’s So Special About PKCS#1 v1.5? And The Attack That Just Won’t Go Away!
事实上这里描述的在情况现实中比较少见，更常见的误用是把加密当作签名，都知道非对称加密速度慢但有不可抵赖，不可伪造的优点，再加上其他信息可添加不可重用不可篡改的能力，而对称加密有速度快的优点，常见的结合就是公钥密码加密对称加密的密钥，而对称加密加密数据，一些人只把证书使用对称密码加密，再使用私钥加密对称密码的密钥，一般认为私钥加密数据就是签名，但此时由于它没有绑定真正数据因此它并没有不可伪造不可篡改的特性，因为它的公钥密码没有保护真正的数据。
举个🌰
1. 误用导致任意证书授权
如下某软件的证书是一个Zip包，它的解析过程是先使用公钥解密获取DES密钥，再用获得的密钥解密证书，因此用户在获取一个合法证书后，即可通过它生成任意合法证书：
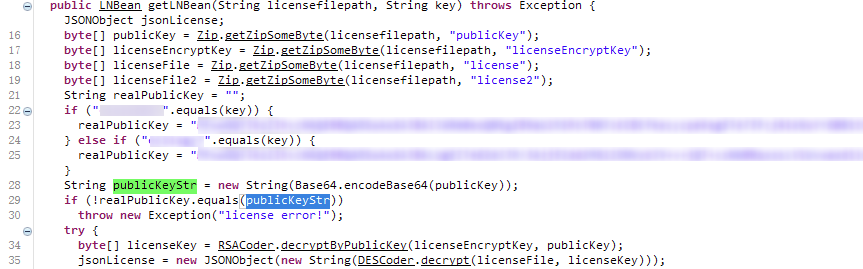
2. 误用导致任意代码执行
如下，某服务收到远端的数据后，会调用如下函数解密，它的解密过程和上图完全一致，因此我们能伪造任意数据：
接下来它将把解密后的数据传入此函数：
可见该函数所做操作是把数据写入某文件，再执行该文件，因此造成了任意代码执行。
如上，当一直合法密文是可轻易伪造数据，而当不知道后合法密文时，由于PKCS1.5要求PS长度不小于8，因此我们需要伪造一条数据，该数据解密后的需要满足0x00||0x02||8个非0||0x00||任意数据的格式，Bleichenbacher分析了当N足够大时我们可以在不知道合法密文时伪造出合法密文，不过现实中大多都会使用标准的e和2048/4096大小的N，另外如果RSA解密实现有误，没有严格检查PS长度，我们也可以轻易的伪造数据，可惜现实中没啥人会自己实现这部分！